Biometry for Intra-Ocular Lens (IOL) Power Calculation

All content on Eyewiki is protected by copyright law and the Terms of Service. This content may not be reproduced, copied, or put into any artificial intelligence program, including large language and generative AI models, without permission from the Academy.

Article initiated by:

Hussain Syed Faraaz Shahzad

All contributors:

Alpa S. Patel, M.D., Jordan Scott Masters, MD, Chris O’Brien, MD MBA, Hussain Syed Faraaz Shahzad, Koushik Tripathy, MD (AIIMS), Derek W DelMonte, MD, Daniel Anderson, MD

Assigned editor:

Daniel Anderson, MD

Review:

Assigned status Up to Date

 by Daniel Anderson, MD on September 18, 2024.

add
Contributing Editors:	add

Biometry

MeSH

D001699

Introduction

Background

Biometry is the method of applying mathematics to biology. The term was originally used by Whewell in the 1800s for calculating life expectancy. The refractive power of the eye primarily depends upon the cornea, the lens, ocular media, and the axial length of the eye. When planning for cataract surgery, in order to achieve the desired post-operative refraction, the required power of the intraocular lens (IOL) implant can be calculated if the corneal refractive power, media type, and axial length are known.

History

In 1949, Harold Ridley implanted the first IOL but his patient had a refractive surprise of nearly 20 diopters. Fyodorov and co-workers first estimated the optical power of an IOL using vergence formulas in 1967. In the 1970s, after availability of accurate “A” scans, several studies were conducted to establish and publish various theoretical vergence formulas. In the early 1980s, several IDEM (ideal emmetropia) lenses were also attempted, so named as the pre- and post – refraction from them were similar. On similar lines, Standard lenses were also attempted, after Gernet and Zorkendorfer in 1982 showed that the average refractive power of natural lens is +23.70D. Although these were neither strictly mathematical nor ethically sound, they should be mentioned for their due respect in a historical perspective. The theoretical formulas derived around the same time have been subjected to minor and major alterations in the variables since then in order to increase accuracy.

Definitions

Outcome

Emmetropia or no refractive error is the ideal outcome sought, in accordance with which maximum biometry is carried out. However, in certain circumstances some may benefit from either a hypermetropic or myopic status postoperatively. In cases where the patient prefers a certain refractive state for either occupational or social needs, including low vision aids. Sometimes the other eye refractive state has to be considered, as in cases of monovision or anisometropia, which should be kept less than 3 diopters.

Refractive State of the Cornea or keratometry (K)

The measurement of corneal power though not absolutely accurate is based upon the steepness of the cornea. The cornea is assumed to be a perfect spherical optical mirror with a fixed anterior to posterior corneal curvature ratio. The cornea then acts as a perfect convex mirror, leading to a virtual image of the target. The corneal curvature is predicted from this, which is then used to determine the corneal power. The basic error in most keratometers is that they do not provide enough information to calculate corneal curvature accurately. Moreover, the cornea must be assumed to be a perfect sphere with par-axial optics, and the power of the back of the cornea must also be estimated (if not calculated with newer posterior imaging techniques) . Computerized videokeratography is now gaining standardization for more accurate results.

Axial length (AL)

Axial length is defined as the distance from the anterior corneal surface to the retinal pigment epithelium. Can be performed using optical or ultrasound methods, which can further be done by direct contact or immersion. A combination of these measurements prevents errors in AL measurements. Optical methods like IOL master have benefits of non-contact procedures along with greater accuracy, but can be inaccurate or difficult to obtain in dense cataracts. Contact ultrasound measurements have been the gold standard earlier, but are likely to have more subjective errors due to corneal compression. Immersion avoids the corneal compression but has less control over alignment, hence can give rise to varied results. Hence a combination of techniques can give better results.

A-constant

A-constant, although called a constant is actually highly variable depending upon multiple factors – IOL dependent: type, material, position; surgeon dependent: technique of incision, placement of incision; K and AL measurement adjustments; or even adjustment for the manner of carrying out biometry. Once fixed for a particular surgeon, IOL and machine for the scan, it is applied as a constant to the appropriate formula. It approximately varies with a ratio of 1:1 with the IOL power.

Gain

Defined as the electronic amplification factor of the sound waves received by the transducer, it is measured in decibel (dB). Normal setting is around 70% -75%. But it may be increased where high echoes are inadequate (hard cataracts, dense ocular opacities, high myopia). It is decreased when artifacts are seen near the retinal spikes (silicone filled eyes & in pseudophakics).

IOL Formulae for calculation

Formula for calculation of IOL power have been evolving since their inception. These can be classified on the basis of their derivation (theoretical, regression analysis or combination) or according to their evolution as per generations. By derivation, theoretical formula are determined by application of geometrical optics to the schematic and reduced eyes using various constants. Later; regression analysis using the actual post-operative results of implant power as a function of the variables of corneal power and axial length were derived. Sanders, Retzlaff and Kraff developed the SRK formula which was widely used. Though now replaced with the newer generation formulas, it is still useful for understanding the relation of the variables and A-constant to the IOL Power (P).

P = A – 0.9 K – 2.5 AL

Where

P= Power of the IOL in diopters

A= A constant

K= Average keratometry value in diopters

AL= axial length in mm

This is rarely used to calculate IOL power manually where other tools are not available, but should be avoided whenever possible. The various generations of formula are discussed under the “Mathematics and Measurements” subheading.

Mathematics and Measurements

Underlying Principles & Parameters

Most of the modern day formulae are based upon the theoretical equation formulated by Fyodorov and its modifications. Here the IOL power is chosen as the variable, which is calculated on the basis of this equation and its derivatives…

               P = (1336/[AL-ELP]) – (1336/[1336/{1000/([1000/DPostRx] - V) + K} - ELP])

Where

• Net corneal power (K)
• Axial length (AL)
• IOL power (P)
• Effective lens position (ELP)
• Desired refraction (DPostRx)
• Vertex distance (V)

The only variable which cannot be measured pre-operatively is ELP and most of the later day formulae like Holladay, Hoffer Q, SRK/T or Haigis attempt to calculate ELP more accurately.

Effective lens position (ELP)

ELP was the term used to denote the position of the lens in the eye- specifically the distance that the principal plane of the IOL will sit behind the cornea. As the older variable, anterior chamber depth (ACD); was found to be inaccurate anatomically for “in the bag” implanted IOL. In accordance with these variables the formulae can be divided as …

The newer modifications have continued since, but the improved accuracy of post-operative refraction is also due to increased surgical proficiency and cataract techniques over the years. Example being the Holladay 2 which uses patient age and preoperative refraction as further variables to improve accuracy; while Haigis replaced K with preoperative ACD to improve accuracy. The Barrett formula additionally incorporates ACD into its calculations.

Using Gaussian reduction equations, the formula for calculating IOL power can also be expressed in accordance with the refractive index…

     P = [nv/(AL - C)] - [K/(l- Kx C/nA )]

where P = power of the target IOL (in diopters [D]) K = average dioptric power of the central cornea (in D) AL = visual axial length (in millimeters) C = ELP (in millimeters), the distance from the anterior corneal surface to the principal plane of the IOL nv = index of refraction of the vitreous nA = index of refraction of the aqueous

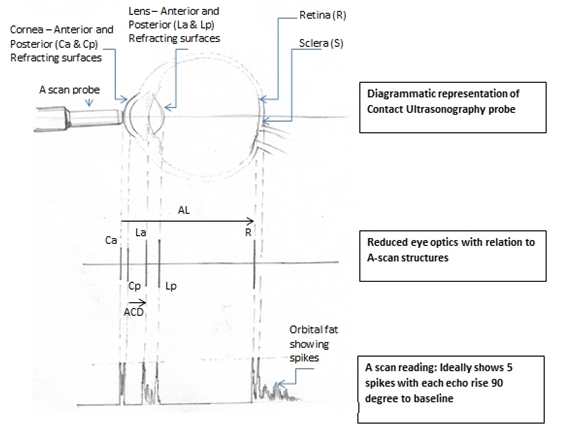
Figure 1 Diagrammatic representation with Reduced Optics correlation and A-scan (Redrawn by Dr F. Hussain, not to scale)

See figure 1, for diagrammatic correlation.

The ELP in the original formulae was a constant, as the lenses used were mostly in the anterior chamber. Hence this was incorporated into the “A” constant in the later regression analysis like SRK. Today, the newer formulae generally use only one constant incorporated as A-constant or Surgeon Factor (SF). The original A-constant developed in the 1980s was so widely used that every lens was designed with a specific A-constant by the manufacturer. Even though regression analysis is not recommended today; the A-constant still remains due to its benefits in emergency usage and manual derivation for confirmation.

Corneal Power (K)

It is considered the second most important factor for IOL power determination. Changes in K reading; alters the IOL power in a ratio of nearly 1:1. It can be measured either by keratometry or topography but neither measures the actual corneal power directly. The mathematical principle behind the keratometry method is that the central cornea is assumed to be a perfect sphere and acts as a spherical convex mirror. Further the posterior corneal curvature is assumed to be 1.2mm steeper than the anterior; this is especially altered after refractive surgeries due to which increased errors are observed. From the size of the reflected image from the cornea acting as a convex mirror, the radius of curvature is determined, which is then converted to power in diopter or mm.

   Radius(r) of curvature (mm) = 2u (mm) multiplied by Size of Image/ Size of Object

u = distance of object from principle plane And

   D = (n2 – n1) / r

n = Refractive index of medium 1 & 2 respectively.

Topographical methods use the Scheimpflug principle via the Pentacam or the Galilei (double Scheimpflug) to measure the anterior and posterior radii of corneal curvature along with the corneal thickness which is then used to measure corneal power in diopters. In a normal phakic eye the average anterior corneal radius of curvature is 7.5mm, which corresponds to 44.44D using keratometric refractive index of 1.3333(4/3) which was found to be more accurate than the older one used 1.3375. The posterior corneal radius of curvature averages 1.2mm less than the anterior surface radius.

Axial Length (AL)

It is perhaps the most important parameter in most modern day formulae. It changes the IOL power by nearly 2.5 to 3 times, more so in short eyes than in longer ones. Can be measured using Ultrasonography (contact or immersion) or Optical methods (IOL Master & Lenstar). Ultrasonography uses mechanical waves to calculate the time needed for a pulse to travel from the cornea to the retina. Sound travels with different speeds as per the media, more in lens and cornea (1641m/s) and less in aqueous and vitreous (1532m/s). This is then converted to distance by

   Distance (m) = time (s) X  velocity (m/s)

Average velocity of a normal phakic eye is 1555 m/s. Ultrasonography methods can be applanation or immersion, the former is more inaccurate due to indentation, but the latter has less control. The A –scan (Amplitude modification) is a one dimensional display in which echoes are represented as vertical spikes from a baseline. Optical Methods use partial coherence laser for AL measurement. Similar to ultrasonography, optical methods also measure time needed for infrared light to travel from cornea to retina, but uses interferometry principle in order to avoid the problem of very high light speed measurements. As it is a non-contact procedure, no indentation errors occur. Two main instruments are available for optical methods IOL Master from Zeiss and the Lenstar from Haag-Streit. It has been reported that there are no statistically significant difference in the measurement of AL by IOL Master, Lesntar and immersion ultrasonography by Montes- Mico. Average AL in a normal phakic eye is about 24mm in adults.

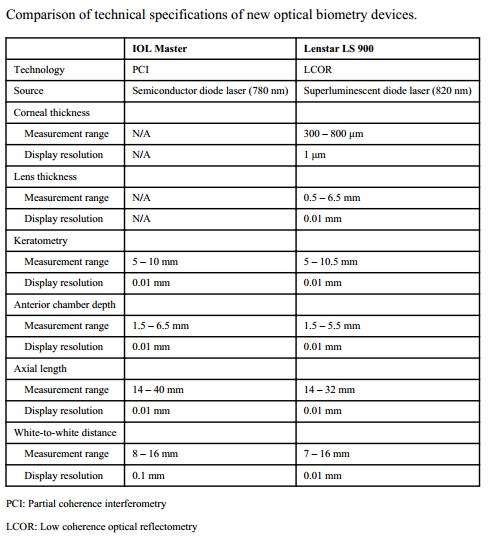
Measurements (IOL Master & Lenstar)

Optical methods of measuring AL need more elaboration as compared to immersion ultrasonography.

Because of these about 8-17 % of eyes cannot be measured using the Optical methods, hence immersion continues to have a role. A comparison between the newer devices for optical methods of measurements is also useful as one must be aware of the available options and their benefits…

From the work of Sahin – Hamrah et al.

Special circumstances

In Aphakia

The parameter altered is the speed of travel of sound, which now averages 1532m/s, and the two lens spikes in A-scan are absent, being replaced by a single spike of the anterior vitreous face and posterior capsule. Immersion method is preferred rather than contact, newer devices have specially programmed modes for aphakia. Most of the values remain similar in the theoretical equations already discussed, except the manufacturer’s ACD and the measured K reading. As the manufacturer’s ACD is for in the bag placement, unless special lenses are utilized, the value should be reduced by 0.25 mm for sulcus placement. For posterior iris fixation a further reduction of ACD by 0.25mm is needed. Similarly the measured K reading must be converted to the net K reading with RI 4/3 or 1.3333.

In Pseudophakia

This can be important for IOL exchange or for comparison while doing biometry for the other eye. Eyes with IOL have an extremely high spike at the lens followed by an artificial chain of reduplication echoes which can be confused with retinal spikes. This is avoided by reducing gain to decrease the artificial spikes and make retinal ones more prominent. The speed of sound travel now depends upon the type of IOL and its parameters. In newer devices prefilled data is available in accordance with the type of implant. Optical Biometry is preferred which offers more accurate correction of the AL by correction factor (CF) which varies as per the lens type and thickness. Common examples: PMMA, the conversion factor is +0.45; for silicone it is either -0.56 or -0.41 (depending on the style and manufacturer); and for acrylic it is +0.30. These must be applied to the formulas

    TAL = AAL 1532 + (cf x t);

Lens thickness (t) must be obtained from the manufacturer.

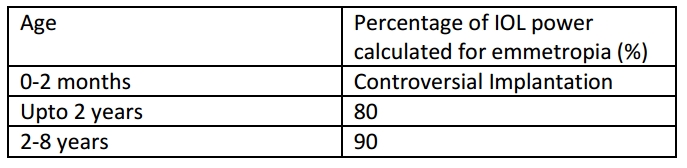
In Pediatric age group

The problems in pediatric age, especially the very young; includes the increased errors in AL measurement, which compounds the final IOL power errors due to shorter AL. AL and K value must be measured under general anesthesia. The IOL power chosen should allow good vision in growing age to prevent amblyopia and ideally also give emmetropia in adult age.

Currently all infants above two years are advised IOL implantation; while some controversy exists in younger ages. The greatest concern at such an early age is to prevent amblyopia. The development of the eye necessitates initial under-correction to avoid later myopic shift. The growth of the anterior segment is usually completed at around two years hence the IOL aimed for is about 80% of the calculated amount of power.

Note: These corrections are to be made on the newer generation formulas like SRK/T.

Piggy back IOLs with one implant being permanent in the bag and the other temporary in the ciliary sulcus has been suggested by Dr. M. Edward, where in the temporary one is removed at adult age.

After Posterior segment Surgery

The major issue is with silicone filled eyes after vitrectomy in which IOL implantation is being considered. The velocity of sound in silicone is slower than in vitreous which must be corrected for measurement of the AL accurately. The two most common types of silicone have different tissue velocities, 1050 or 980 m/s; hence one must know which velocity to select to avoid a small mistake in axial length. This is usually achieved after alteration of settings in the newer machines.

Moreover silicone in the eye itself acts as a negative lens when a biconvex IOL is implanted hence the IOL power must be adjusted by 3-5 D. Measurement adjustment to improve accuracy can also be achieved by calculating each segments ratio and then obtaining the IOL value by appropriate alteration. Measurement of AL by optical method has been found to much more accurate for silicone filled eyes.

After Refractive Surgery

Corneal Refractive surgeries alter the basic assumptions on which the biometry for IOL calculations is based – namely the perfectly spherical nature of cornea. The refractive surgeries mainly affect the central cornea, as well as alter the posterior corneal curvature, which is not routinely measured. The errors occur due to instruments, index of refraction and formulas used.

Instrument errors occur due to the inability of keratometers to measure the central zone of effective corneal power. While they measure a 3.2mm zone diameter, this misses the central effective zone. Flatter the cornea, greater the measurement zone hence greater the error.

Refractive index (RI) is based upon the ratio between the anterior and posterior corneal curvatures. As may be recalled most instruments only measure the anterior curvature while making assumptions about the posterior curvature to derive at the RI, hence K. The relationship between the curvatures is altered in PRK, LASIK & LASEK, but avoided in RK which causes alteration of curvatures such that the relation is maintained. This overestimates the corneal power by 1D for every 7D of correction of refractive error.

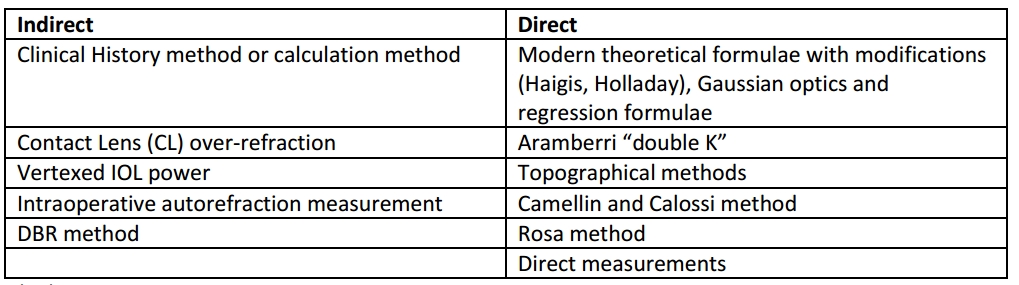
Formulas error occurs in nearly all modern ones like Holladay, SRK/T (but not in Haigis), all of which use the AL & K to predict ELP post-operatively. As the other dimensions of the anterior chamber are not altered proportional to the central cornea after the refractive surgeries, this prediction leads to erroneous results. Methods to measure IOL post-Refractive surgery can be divided as “Indirect” or “Direct” based on the measurement of the corneal power after surgery (direct involves actual measurement, while indirect makes assumptions based on historical data or theoretical analysis.)

Indirect

So named because they utilize measurement apart from post-refractive surgery corneal power reading.

Clinical History or Calculation method

Needs 3 parameters:

• Pre-op K
• Pre-op Refraction
• Stabilized refraction after keratorefractive procedure.

The stabilized refraction must be measured before changes in refraction occur due to cataractous alterations.

Here,

               K postReSx = K preReSx – difference in Spherical Equivalent

{ReSx = Refractive surgery}

It is most accurate as the pre-op values are precise up to +/-0.25mm .

Contact Lens over-refraction

Needs 4 parameters:

• Base curve of contact lens in Diopters (BC)
• Power of contact lens (P)
• Manifest refraction (MRx) before ORx

This formula is:

          K postReSx = BC + P + (ORx - MRx)

The limitation is the reliability of refraction in the patient with cataract .

Vertexed IOL method

Based on theoretical studies by Feiz, Latkany and their colleagues, various nomograms were developed after calculating IOL power post LASIK with SRK/T and three other formulas. The change in the spherical equivalent after LASIK was used to modify the IOL power. Its main limitation is the theoretical nature of the study and the lack of large published data with regards to its accuracy.

Intraoperative auto-refraction measurement

It directly uses intraoperative refraction data to calculate the IOL power, without need of knowing AL and K. A special “A-constant” is formulated for the same. Main limitation is the lack of support by large data studies .

DBR Method

Like the calculation method, needs data from both before and after surgery…

Pre-operative:

• Refraction
• Keratometry
• AL
• IOL Power for emmetropia

Post-operative:

• Refraction plane
• Residual refractive error after stabilization of refraction

               0.7D change at spectacle plane = 1.0D change at IOL plane. 

This co-relation is then used to obtain the IOL power post refractive surgery .

Direct methods

So named as one actually measure the corneal power post-operatively to calculate the effective keratometric diopters. Although most modern devices do not directly measure the posterior corneal curvature, they use alternative algorithms to approximately assume the RI change induced or simply use different variables to predict ELP .

Gaussian optics and linear regression

The Gaussian formula uses:

• Anterior & Posterior radius of curvature
• RI of air (1.0); of Anterior K (1.376) & of Aqueous humour (1.336)
• Corneal thickness

To calculate the Effective Refractive Power (EffRP), the posterior corneal curvature is not directly measured but predicted from the data of Oslen et al. . EffRP was then used to predict ELP, along with the application of linear regression analysis . Errors of nearly 0.5 D are still noted.

Topography method

It uses the keratometric reading and the flattest corneal power in the central 3mm zone to calculate the simulated K (SimK). This is then used to predict ELP. Errors occur due to central zone giving steeper K values .

Maloney topographic method uses SimK from topography and applies it to the formula

          K = 376/ (337.5/SimK) – 5.5

This K reading then predicts the IOL power.

Aramberri “double K” method

Aramberri reported in 2002 that the flatter K should not be used in modern formulae. The pre-operative K is used to predict ELP while the post-operative K is incorporated in the formula for actual IOL power prediction. This was later incorporated in the Holladay 2 vergence calculation formula .

Camellin and Calossi

They reported a formula which uses induced refractive change as well as anterior and posterior curvature of cornea to predict IOL power.

Rosa method

This uses a correction factor (R factor) for corneal radius which was derived from a regression formula and then compared with the calculation method and double K method. In their study of 19 eyes R factor was found to be superior when applied to the SRK/T and Holladay 1. The actual formula for IOL power is derived from manual measurements of corneal power (K) and axial length (AL).

              K = (0.0276 x AL + 0.3635) manual K 

Direct measurements of Anterior & Posterior corneal power

With the invention of these newer instruments direct measurement of the posterior corneal power is also possible, which then gives more accurate results for IOL calculation after refractive surgery. The Orbscan and the Pentacam both have been used to measure posterior corneal power, with the Pentacam having slight advantage. But these need more study and data .

Despite the various methods described, the science of IOL power calculation after refractive surgery is still in its nascent stages and needs more research. Generally calculation method is considered most accurate, followed by corneal topography and automated K.

In Corneal Transplants

It is extremely difficult to accurately predict corneal power in transplant patients. If a triple procedure is planned it is suggested that K readings of other eye be used. An alternative option is to use the average k readings from a series of previous transplants. If there is a corneal scar, but no graft is planned, other eye readings can be used or even the power calculated using AL and refractive error of affected eye .

For Piggy-back IOLs

In patients with post IOL refractive surprise or in those with large dioptric requirement, a piggy back IOL in sulcus can be placed along with the primary implant. This method does not require knowledge of the power of the primary implant or of the axial length. Minor adjustments are needed, which can be achieved using these formulae:

• Myopic correction: P = 1.0 x Error
• Hyperopic correction: P = 1.5 x Error
• where
• P = the needed power in the piggyback lens
• Error = the residual refractive error that needs to be corrected

Errors and Mistakes

Common pitfalls

Limits of Biometry

It has to be acknowledged that calculation of IOL power is not absolute due to the large number of individual variations in human eyes. Major sources of error have been documented in a study by Norrby et al…

Sources of error can also be due to acts of omission and commission

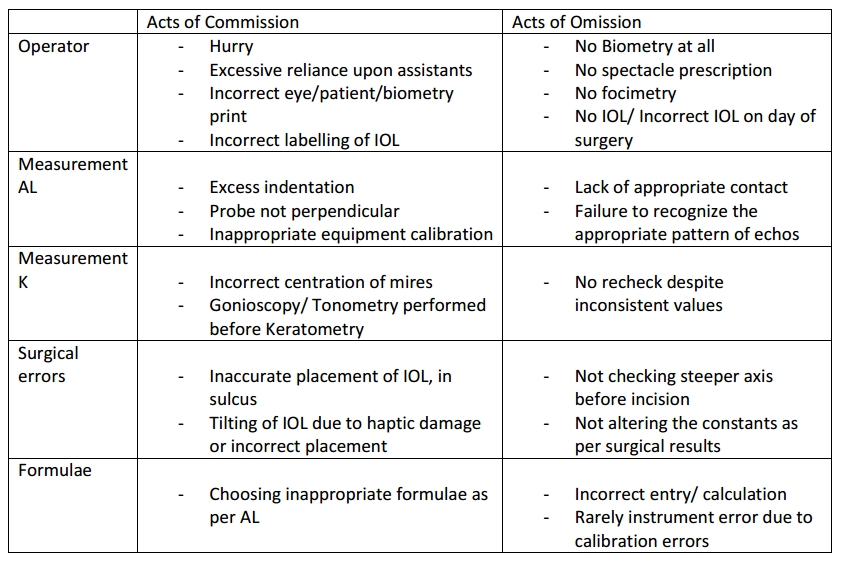
Improving outcomes

Albeit not perfect, biometry for IOL power calculation can be made very precise, if one follows simple guidelines.

Patient counselling and requirements

All patients may not want emmetropia and some it may not be possible to ensure the same pre-operatively, as in very dense cataracts where macular lesions can be missed. Counselling the patient well is a must; who should be informed and then offered the options as per his/her needs.

General guidelines

Each surgeon must review their own results and appropriately make alterations to biometry if needed. Regular checks and audits are a good habit. Training and monitoring the staff is equally important. While selecting the patient, ensure the eye and the papers are in order and correspond to each other. Cross checking with refraction is also a good adjunct if accurate retinoscopy is available. While performing the actual scan, ensure asepsis, especially in contact procedures. Patient comfort and appropriate anesthesia should be monitored.

AL measurement

Optical ultrasound is the gold standard for AL measurement due to ease of use, accuracy and reproducibility as well the non-contact nature of the procedure. As it cannot be accurate in certain conditions already seen, it can be supplemented with ultrasonography methods to improve outcomes. Immersion is preferred as it approaches the accuracy of optical methods, but is cumbersome to use. In cases where it is not available contact ultrasonography is still utilized. Appropriate machine calibration is necessary before the scan itself.

Good A-Scan graph: (see figure 1)

• Corneal echo is seen as a tall single spike
• No echoes from Aqueous humour
• Anterior and Posterior lens capsule produce tall echoes
• No echoes from Vitreous cavity
• Retina produces tall sharply rising spike with no staircase at origin
• Orbital fat produces medium to low echoes
• Check A-scan graphs: If the spike from retina is not followed by multiple small spikes it means one is hitting optic nerve, so discard that reading.
• If there is a reading where the anterior chamber depth and actual length reduces, it indicates that in that particular reading one is compressing the cornea. It should be discarded.
• Gain should be the minimum possible which gives good spikes.
• Average of 8-10 measurements increases accuracy

Some useful tips for contact procedures:

• Probe should be perpendicular, centered and pointing towards macula.
• No fluid between probe and cornea
• No depression of cornea

K measurement

Can be calculated by either using automated or manual method. Performing a double check by both methods helps in improving accuracy.

Useful tips:

• No other contact procedure before keratometry
• Use topical anesthetic before scan
• Calibrate keratometer before scan
• Take an average of 3 readings
• If discrepancy, ask a second person to cross check
• Compare the refraction, especially the axis with the K values
• Repeat if difference is more than 1.0D between the two eyes.

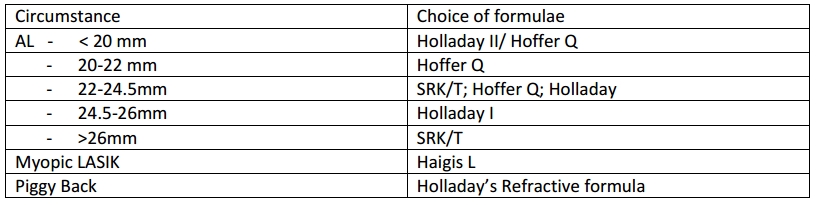
Choice of formulas

Albeit controversial, some guidelines have been developed for which formulae to use under specific circumstances. Although earlier widely used, the SRK 2 and older ones now obsolete. Appropriate calibration of settings and adjustments of constants is a must before IOL power prediction. No single formulae has been found to be useful in all circumstances.

The newer formulae like T2 modification of SRK/T; Oslen’s formula, Hollady 2 and Haigis are still not widely available in the biometry software. Due to the absence of compelling comparative evidence of the superiority of these formulas over each other, it is justifiable to continue using an appropriate combination (according to axial length) of the two variable - single constant formulas.

Future Trends

As technology and patient expectation increases, one must continue to look to improve our own precision.

Formulas

Holladay IOL consultant (HIC) program uses Holladay 2 formula and performs complex power calculation for the surgeon. It has various other new features, but it still not widely available. Oslens’s formula uses pre-operative refraction and lens thickness for increasing accuracy. The newer vergence-based formula, the Barrett II universal, utilized 5 variables and has greatly increased post cataract surgery refractive outcomes over older formulas. Additionally, the artificial intelligence powered formal Hill-RBF, shows great promise in optimizing refractive outcomes in the future.

Software based: Okulix

A new biometric computer program to stimulate whole pseudophakic eye aims to reduce calculation error and ensure a more reliable estimation of IOL strength. This approach separates the errors due to measurement and those due to calculation, helping us in correcting them better. The Olsen and Okulix formulae utilize ray-tracing, which adds the benefit of accounting for aberrations throughout the visual system.

Newer Machines:

The Pentacam and Orbscan have already been used widely for corneal ectasia, but are now beginning to be utilized for precise corneal power measurements.

Intraoperative aberrometry is now being used as a way to confirm and improve accuracy of IOL calculations. The Optiwave Refractive Analysis device (ORA by Alcon) is one example of this. It has been shown to be at least equal to more the more advanced Barrett and Hill-RBF formulas, but may have special use in complex cases such as post-refractive and toric IOLs.

IOL with tolerance

It has been suggested that manufacturers reduce the internal – tolerance levels of IOLs to +/- 0.25D, thereby increasing accuracy. However, these parameters are not routinely provided by manufacturers to clinicians.

Additional Resources

Many options are now available for references as well as direct IOL calculations. Some of these are listed below.

Online options

• http://www.doctor-hill.com/physicians/download.htm

Offline Options

• http://en.osdn.jp/projects/sfnet_eyecalculator/
• The eye calculator software can be very useful in training institutes as it is usable offline as well.

References

52. Binkhorst RD. Intraocular lens power calculation manual. A guide to the author’s TI 58/59 IOL power module. 2nd ed. New York: Richard D Binkhorst; 1981.
53. Ram J, Pandav SS, Ram B, et al. Systemic disorders in age related cataract patients. Int Ophthalmol 1994;18:121–5.
54. Ianchulev T, Salz J, Hoffer K, et al. Intraoperative optical refractive biometry for intraocular lens power estimation without axial length and keratometry measurements. J Cataract Refract Surg 2005;31: 1530–6.